My Luck Could Change Tomorrow

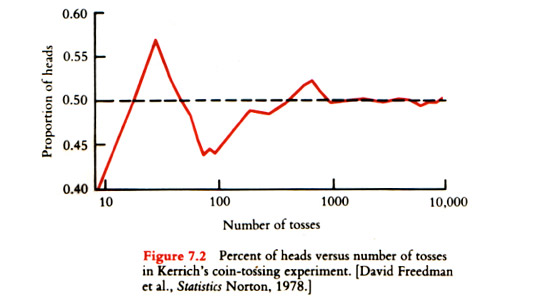
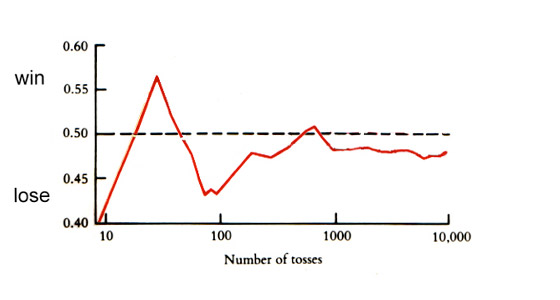
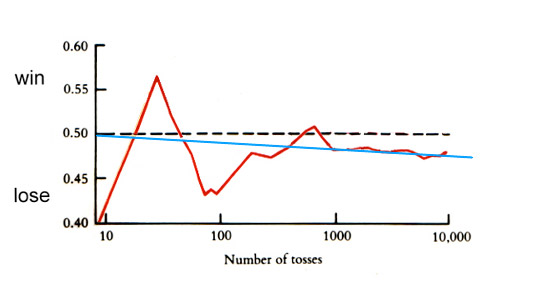
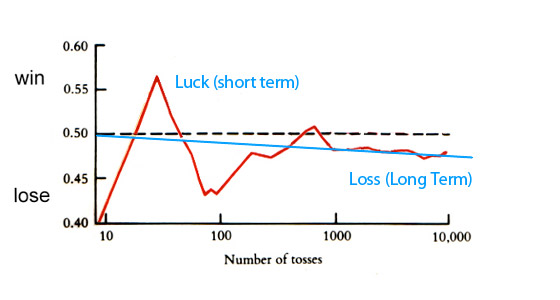
John Kerrich1, an English mathematician, wanted to explore the pattern of random phenomena. While interned by the Germans in World War II, he tossed a coin not once, but 10,000 times. What did he discover? Kerrich’s first 10 tosses gave 4 heads, a proportion of 0.4 or 40%. After 20 tosses the proportion of heads increased to 50% and after 30 tosses, 57%. In a small number of tosses the number of times heads came up was unpredictable. But after Kerrich threw the coin 5000 times a proportion of 50.7% heads resulted. Many tosses produced a smoothing effect. And in all 10,000 trials, he scored 5067 heads, or 50.67% heads.

The proportion after 100,000 would be even closer to the true probability of 50%.

Note that the number of tosses is on a logarithmic scale, for clarity.

A similar pattern would hold if we were gambling regularly on red or black at roulette, or at a poker machine – but the house edge has to be included, which skews the red line downward. The more the house edge, the more the line angles down:

The blue line is an ‘average return:’

We can now see that ‘luck’ holds in the short term, as the results are unpredictable. In the long term however, the law of large numbers holds true. This is how the casino makes its profits – from the many, many plays and the house edge; the maths guarantees that the casino will ‘win’.

As a player moves from an occasional player to a long term or regular player, the same maths applies. For the regular player, the more you play, the more you are likely to lose.

While a regular player may look to tomorrow for better luck, it is clear that any good luck would be a minor variation against a remorseless pattern of loss.

1. From For All Practical Purposes. Introduction to Contemporary Mathematics Consortium for Mathematics and Its Applications. W H Freeman and Company New York 1988. Graphs 2, 3 and 4 have been adapted for the discussion. – See more at: https://knowyourodds.net.au/my-luck-could-change-tomorrow/#sthash.xqMULt5i.dpuf